
1.2 Bouncing Cosmology and cyclic models
Bouncing cosmology and cyclic models share similarities, but they are not the same. Both propose an alternative to the standard Big Bang model by suggesting that the universe undergoes a series of cycles consisting of expansion and contraction phases. However, the mechanisms and details of these cycles can vary between different bouncing cosmologies and cyclic models.
Bouncing cosmology is a broader concept that encompasses various models in which the universe experiences a transition from a contracting phase to an expanding phase, avoiding the initial singularity problem. The bounce can be achieved through different mechanisms, depending on the specific model. Some bouncing cosmologies are based on classical general relativity, while others incorporate elements from quantum mechanics or string theory.
Cyclic models, on the other hand, are a specific type of bouncing cosmology in which the universe undergoes a series of cycles that include alternating expansion and contraction phases. One of the most well-known cyclic models is the ekpyrotic/cyclic universe, which is inspired by string theory and brane cosmology. In this model, the bounce occurs due to the collision of higher-dimensional branes, and the cycles continue indefinitely.
Bouncing cosmology is a collection of cosmological models that propose that the universe undergoes a bounce or transition from a contracting phase to an expanding phase, avoiding the initial singularity problem. Various bouncing cosmology models are based on different frameworks and mechanisms. Here's an overview of some notable models:
1.2.1 Ekpyrotic and Cyclic Models:
The original ekpyrotic models relied on string theory, branes and extra dimensions, but most contemporary ekpyrotic and cyclic models use the same physical ingredients as inflationary models (quantum fields evolving in ordinary space-time). Like Big Bang cosmology, the ekpyrotic theory has accurately described essential features of our universe. It predicts a uniform, flat universe with patterns of hot spots and cold spots, in agreement with observations of the cosmic microwave background (CMB), observations confirmed to higher precision by the WMAP and Planck satellite experiments. [10] Observation of a CMB has long been considered evidence of the Big Bang, [9] but proponents of the ekpyrotic and cyclic theories contend that the CMB is also consistent with a Big Bounce as posited in those models. [11] Other researchers argue that data from the Planck observations of the CMB "significantly limit the viable parameter space of the ekpyrotic/cyclic scenarios." [12]
1.2.2 Loop Quantum Cosmology:
Loop quantum cosmology (LQC) is a finite, symmetry-reduced model of loop quantum gravity (LQG) that predicts a "quantum bridge" between contracting and expanding cosmological branches.
The distinguishing feature of LQC is the prominent role played by the quantum geometry effects of loop quantum gravity (LQG). In particular, quantum geometry creates a brand new repulsive force which is totally negligible at low space-time curvature but rises very rapidly in the Planck regime, overwhelming the classical gravitational attraction and thereby resolving singularities of general relativity. Once singularities are resolved, the conceptual paradigm of cosmology changes and one has to revisit many of the standard issues—e.g., the "horizon problem"—from a new perspective.
Since LQG is based on a specific quantum theory of Riemannian geometry, [14 ] [15] geometric observables display a fundamental discreteness that play a key role in quantum dynamics: while predictions of LQC are very close to those of quantum geometrodynamics (QGD) away from the Planck regime, there is a dramatic difference once densities and curvatures enter the Planck scale. In LQC the Big Bang is replaced by a quantum bounce.
Study of LQC has led to many successes, including the emergence of a possible mechanism for cosmic inflation, resolution of gravitational singularities, as well as the development of effective semi-classical Hamiltonians.
This subfield originated in 1999 by Martin Bojowald, and further developed in particular by Abhay Ashtekar and Jerzy Lewandowski, as well as Tomasz Pawłowski and Parampreet Singh, et al. In late 2012 LQC represented a very active field in physics, with about three hundred papers on the subject published in the literature. There has also recently been work by Carlo Rovelli, et al. on relating LQC to spinfoam cosmology.
However, the results obtained in LQC are subject to the usual restriction that a truncated classical theory, then quantized, might not display the true behaviour of the full theory due to artificial suppression of degrees of freedom that might have large quantum fluctuations in the full theory. It has been argued that singularity avoidance in LQC are by mechanisms only available in these restrictive models and that singularity avoidance in the full theory can still be obtained but by a more subtle feature of LQG.[16] [17]
1.2.3 Matter Bounce Scenario
In this model, the bounce occurs due to the effects of regular matter, rather than inflation driven by an exotic scalar field. The universe contracts under the influence of gravity until the matter density reaches a critical value, causing a bounce and a subsequent expanding phase. This model explains the observed large-scale structure and homogeneity of the universe without invoking inflation.
1.2.4 String Gas Cosmology
Although not strictly bouncing cosmology, string gas cosmology is related to the idea of avoiding an initial singularity. This model, based on string theory, posits that the universe emerged from a dense gas of fundamental strings in thermal equilibrium. The interactions and dynamics of these strings could lead to a phase of contraction before the observed expansion.
1.2.5 Emergent Universe Models
These models propose that the universe existed as an eternal static state or a slowly evolving state before the expansion phase began. The static or quasi-static phase might have lasted indefinitely before transitioning into the expanding phase we observe today. In these models, the universe has no initial singularity and no precise beginning.
Each of these bouncing cosmology models proposes different mechanisms to explain the bounce and offers alternative scenarios for the universe's history before the expansion phase. However, it is essential to recognise that these models are currently speculative and lack direct experimental evidence.
Literature
-
Paul J. Steinhardt and Neil Turok. The Cyclic Universe: An Introduction to the Cyclic Model of the Universe, provides a overview of the cyclic model, including its history, key concepts, and current research.
-
Jean-Luc Lehners. Eternal Inflation With Non-Inflationary Pocket Universes. Provides a detailed overview of the cyclic model, as well as other alternative theories of the origin of the universe, such as the multiverse and the string landscape.
-
Martin Rees. Before the beginning. Simon & Schuster. This book covers a wide range of topics related to the Big Bang theory and its alternatives, including the cyclic model, in an accessible and engaging way.
-
A.S. Agrawal, B. Mishra, P.K. Agrawal. Matter Bounce Scenario in Extended Symmetric Teleparallel Gravity. (2022)
-
Payel Sarkar, Prasanta Kumar Das. Matter bounce scenario in modified f(R,T) gravity. (2023)
-
Robert Brandenberger. The Matter Bounce Alternative to Inflationary Cosmology. (2022)
-
Jaume de Haro and Jaume Amoros. Viability of the Matter Bounce Scenario. (2014)
-
Yu-Bin Li, Jerome Quintin, Dong-Gang Wang, and Yi-Fu Cai. Matter bounce cosmology with a generalized single field: non-Gaussianity and an extended no-go theorem. (2017)
-
Special Issue "Bounce Cosmology". MDPI Universe Journal. (2021)
1.3 String Cosmology
1.3.1 General Overview
String cosmology is a branch of theoretical physics that describes the early universe's history using the principles of string theory. String theory is a theoretical framework that suggests that the fundamental building blocks of the universe are one-dimensional objects called "strings," rather than point-like particles.
This approach can be dated back to a paper by Gabriele Veneziano[1] that shows how an inflationary cosmological model can be obtained from string theory, thus opening the door to a description of pre-Big Bang scenarios.
The idea is related to a property of the bosonic string in a curve background, better known as nonlinear sigma model. First calculations from this model[2] showed as the beta function, representing the running of the metric of the model as a function of an energy scale, is proportional to the Ricci tensor giving rise to a Ricci flow. As this model has conformal invariance and this must be kept to have a sensible quantum field theory, the beta function must be zero producing immediately the Einstein field equations. While Einstein equations seem to appear somewhat out of place, nevertheless this result is surely striking showing as a background two-dimensional model could produce higher-dimensional physics. An interesting point here is that such a string theory can be formulated without a requirement of criticality at 26 dimensions for consistency as happens on a flat background. This is a serious hint that the underlying physics of Einstein equations could be described by an effective two-dimensional conformal field theory. Indeed, the fact that we have evidence for an inflationary universe is an important support to string cosmology.
In the evolution of the universe, after the inflationary phase, the expansion observed today sets in that is well described by Friedmann equations. A smooth transition is expected between these two different phases. String cosmology appears to have difficulties in explaining this transition. This is known in the literature as the graceful exit problem.
An inflationary cosmology implies the presence of a scalar field that drives inflation. In string cosmology, this arises from the so-called dilaton field. This is a scalar term entering into the description of the bosonic string that produces a scalar field term into the effective theory at low energies. The corresponding equations resemble those of a Brans–Dicke theory.
Analysis has been worked out from a critical number of dimension (26) down to four. In general, one gets Friedmann equations in an arbitrary number of dimensions. The other way round is to assume that a certain number of dimensions is compactified producing an effective four-dimensional theory to work with. Such a theory is a typical Kaluza–Klein theory with a set of scalar fields arising from compactified dimensions.
1.3.2 Technical description
The starting point is the Polyakov action, which can be written as
where is the Ricci scalar in two dimensions, Φ the dilaton field, and α’ the string constant. The indices a, b range over 1,2, and μ,ν over 1,…,D, where D the dimension of the target space. A further antisymmetric field could be added. This is generally considered when one wants this action generating a potential for inflation. [18] Otherwise, a generic potential is inserted by hand, as well as a cosmological constant.
The above string action has a conformal invariance. This is a property of a two dimensional Riemannian manifold. At the quantum level, this property is lost due to anomalies and the theory itself is not consistent, having no unitarity. So it is necessary to require that conformal invariance is kept at any order of perturbation theory. Perturbation theory is the only known approach to manage the quantum field theory. Indeed, the beta functions at two loops are
and
The assumption that conformal invariance holds implies that
producing the corresponding equations of motion of low-energy physics. These conditions can only be satisfied perturbatively, but this has to hold at any order of perturbation theory. The first term in is just the anomaly of the bosonic string theory in a flat spacetime. But here there are further terms that can grant compensation of the anomaly also when , and from this cosmological models of a pre-big bang, scenario can be constructed. Indeed, this low energy equations can be obtained from the following action:
where is a constant that can always be changed by redefining the dilaton field. One can also rewrite this action in a more familiar form by redefining the fields (Einstein frame) as
and using one can write
where
This is the formula for the Einstein action describing a scalar field interacting with a gravitational field in D dimensions. Indeed, the following identity holds:
where is the Newton constant in D dimensions and the corresponding Planck mass. When setting in this action, the conditions for inflation are not fulfilled unless a potential or antisymmetric term is added to the string action, [18] in which case power-law inflation is possible.
Literature :
-
String theory and pre-big bang cosmology. M. Gasperini and G. Veneziano (2016)
-
String theory in the early universe. Rhiannon Gwyn (2009)
1.4 Quantum Cosmology
Classical cosmology, fundamentally grounded in Albert Einstein's General Theory of Relativity (GTR or GR), provides an effective representation of the universe's evolution. The GTR, however, reaches its limits when it comes to the conditions of the Big Bang. It struggles to adequately explain the gravitational singularity and the Planck epoch - two areas that are critical for a comprehensive theory of space and time. As a result, the need for a theory that synthesizes the principles of relativity and quantum physics arises.
Several approaches have been pursued in this regard, such as loop quantum cosmology, loop quantum gravity, string theory, and causal set theory. These theories represent the forefront of attempts to integrate relativity and quantum mechanics.
In quantum cosmology, a radical departure from classical concepts is made - the universe is conceptualized not as classical spacetime, but as a wave function. This alternative perspective allows for the exploration of quantum states of the universe itself, opening up new avenues of understanding and potentially solving the complexities inherent in the earliest moments of the universe.
This approach seeks to explain the behavior of the universe at extremely small scales and high energies, where classical physics, like general relativity, fails to provide accurate descriptions. In the context of pre-Big Bang scenarios, quantum cosmology offers several key ideas to explain the early universe's evolution:
1.4.1 Quantum fluctuations
In the field of quantum physics, a phenomenon known as a quantum fluctuation - also termed vacuum state fluctuation or vacuum fluctuation - is characterized by a temporary, stochastic variation in the energy quantity at a specific point in space. This concept arises from Werner Heisenberg's uncertainty principle.
Quantum fluctuations are infinitesimal, random oscillations in the field values that symbolize elementary particles. These include electric and magnetic fields that embody the electromagnetic force conveyed by photons, W and Z fields associated with the weak force, and gluon fields linked to the strong force.
These vacuum fluctuations materialize in the form of virtual particles, which are invariably produced in pairs of particle and antiparticle. Intriguingly, these entities are spontaneously created, devoid of an identifiable energy source, leading to a perceived infringement of energy conservation. However, this violation is theoretically permissible due to the short-lived existence of these particles, which annihilate each other within a timeframe delineated by the uncertainty principle, thereby making them indirectly observable.
The uncertainty principle states the uncertainty in energy and time can be related by ΔE Δt ≥ 1½ħ where 1½ħ ≈ 5.27286×10−35 Js. This means that pairs of virtual particles with energy ΔE and lifetime shorter than Δt are continually created and annihilated in empty space. Although the particles are not directly detectable, the cumulative effects of these particles are measurable. For example, without quantum fluctuations, the "bare" mass and charge of elementary particles would be infinite; from renormalization theory the shielding effect of the cloud of virtual particles is responsible for the finite mass and charge of elementary particles. Another consequence is the Casimir effect. One of the first observations which was evidence for vacuum fluctuations was the Lamb shift in hydrogen. In July 2020, scientists reported that quantum vacuum fluctuations can influence the motion of macroscopic, human-scale objects by measuring correlations below the standard quantum limit between the position/momentum uncertainty of the mirrors of LIGO and the photon number/phase uncertainty of light that they reflect.
As far as the big bang is concerned there are different schools of thought (but discriminating experimentally between those different scenarios is probably not possible and hence we can never really know the thruth:
There is only one universe (hence the “uni”), the big bang happened spontaneously out of nowhere.
Our universe is just one of many, this is called the multiverse. Even here there are different scenario’s:
There is a universal background spacetime (flat) and there are continuously new universes born out of it. Each universe starts as a background fluctuation (a small bubble) and then expands rapidly. Think of this as boiling water where water=the background and bubble= a universe. This is called eternal inflation.
-
There is a variation on this scheme where 2 bubbles (universes) collide. This destroys the 2 bubbles in a big fiery explosion (= big bang) and creates a new bubble (universe).
In String theory the multiverse is a higher dimensional space in which branes (=universes) float around and sometimes 2 branes collide in big fiery explosion (=big bang) and create a new brane.
1.4.2 Quantum gravity
At the Planck scale (around 10⁻³⁵ meters), the effects of gravity become comparable to other fundamental forces, and a quantum description of gravity is needed. Quantum gravity theories, such as loop quantum gravity and string theory, aim to provide a consistent framework for understanding the early universe when the classical description of gravity is inadequate.
In an effective field theory, all but the first few of the infinite set of parameters in a nonrenormalizable theory are suppressed by huge energy scales and hence can be neglected when computing low-energy effects. Thus, at least in the low-energy regime, the model is a predictive quantum field theory.[19] Furthermore, many theorists argue that the Standard Model should be regarded as an effective field theory itself, with "nonrenormalizable" interactions suppressed by large energy scales and whose effects have consequently not been observed experimentally.[26] Works pioneered by Barvinsky and Vilkovisky [20] [21] [22] [23] suggest as a starting point up to second order in curvature the following action, consisting of local and non-local terms:
where μ is an energy scale. The exact values of the coefficients c₁, c₂, c₃ are unknown, as they depend on the nature of the ultra-violet theory of quantum gravity. ln(◻/μ²) is an operator with the integral representation
By treating general relativity as an effective field theory, one can actually make legitimate predictions for quantum gravity, at least for low-energy phenomena. An example is the well-known calculation of the tiny first-order quantum-mechanical correction to the classical Newtonian gravitational potential between two masses.[19] Moreover, one can compute the quantum gravitational corrections to classical thermodynamic properties of black holes, most importantly the entropy. A rigorous derivation of the quantum gravitational corrections to the entropy of Schwarzschild black holes was provided by Calmet and Kuipers.[24] A generalisation for charged (Reissner–Nordström) black holes was subsequently carried out by Campos Delgado.[25]
1.4.3 Quantum tunneling
Quantum tunnelling is a phenomenon in quantum mechanics where particles penetrate a potential energy barrier that they would not be able to surmount under the laws of classical physics. This process is linked to the inherent uncertainty and probabilistic nature of quantum systems.
One way quantum tunnelling may have played a role in the creation of the universe is through a theory known as "quantum tunnelling from nothing," proposed by Alexander Vilenkin. According to this theory, the universe could have originated from a quantum tunnelling event, starting from a state where there was absolutely nothing (not even spacetime), and then a small, closed universe tunnelled into existence, followed by an inflationary period that expanded it to a large size. This is a speculative theory and represents just one of many approaches to the question of the universe's origin.
Quantum tunnelling is also a crucial component of the theory of cosmic inflation. In the context of inflation, the universe is thought to have been in a high-energy false vacuum state shortly after the Big Bang. It could then have transitioned, via quantum tunnelling, to a lower-energy true vacuum state. This process would have been accompanied by a release of energy, driving the rapid expansion of the universe. This is known as the "decay of the false vacuum."
1.4.4 The wave function of the universe
The Hartle–Hawking state is a proposal in theoretical physics concerning the state of the Universe prior to the Planck epoch. It is named after James Hartle and Stephen Hawking.
Hartle and Hawking suggest that if we could travel backwards in time towards the beginning of the Universe, we would note that quite near what might otherwise have been the beginning, time gives way to space such that at first there is only space and no time. According to the Hartle–Hawking proposal, the Universe has no origin as we would understand it: the Universe was a singularity in both space and time, pre-Big Bang. However, Hawking does state "...the universe has not existed forever. Rather, the universe, and time itself, had a beginning in the Big Bang, about 15 billion years ago.", but that the Hartle–Hawking model is not the steady state Universe of Hoyle; it simply has no initial boundaries in time or space. [27] [28] [29]
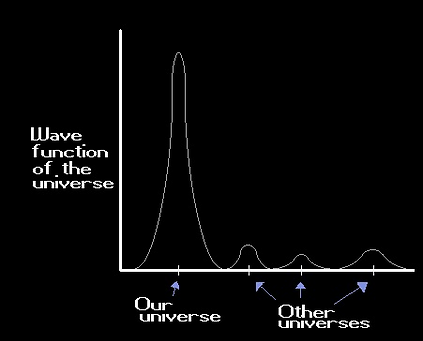
The Hartle–Hawking state is the wave function of the Universe—a notion meant to figure out how the Universe started—that is calculated from Feynman's path integral.
More precisely, it is a hypothetical vector in the Hilbert space of a theory of quantum gravity that describes this wave function.
It is a functional of the metric tensor defined at a (D − 1)-dimensional compact surface, the Universe, where D is the spacetime dimension. The precise form of the Hartle–Hawking state is the path integral over all D-dimensional geometries that have the required induced metric on their boundary. According to the theory, time, as it is currently observed, diverged from a three-state dimension after the Universe was in the age of the Planck time [30]
Such a wave function of the Universe can be shown to satisfy, approximately, the Wheeler–DeWitt equation.
Literature : The wave function of the universe. George Flinn Dissertation. Imperial College London
1.4.5 Inflation
In quantum cosmology, the inflationary paradigm posits that the universe underwent a rapid expansion in its earliest moments, driven by the potential energy of a scalar field called the "inflaton." This inflationary period could help explain the observed uniformity of the cosmic microwave background radiation and the large-scale structure of the universe. Quantum fluctuations during this inflationary phase might have served as the seeds for cosmic structures that emerged later. More about inflation in the chapter Inflationary Epoch.
1.4.6 Quantum bounce
The concept of the Big Bounce envisions the Big Bang as the beginning of a period of expansion that followed a period of contraction. In this view, one could talk of a Big Crunch followed by a Big Bang, or more simply, a Big Bounce. This suggests that we could be living at any point in an infinite sequence of universes, or conversely the current universe could be the very first iteration. However, if the condition of the interval phase "between bounces", considered the 'hypothesis of the primeval atom', is taken into full contingency such enumeration may be meaningless because that condition could represent a singularity in time at each instance, if such perpetual return was absolute and undifferentiated.
The main idea behind the quantum theory of a Big Bounce is that, as density approaches infinity, the behaviour of the quantum foam changes. All the so-called fundamental physical constants, including the speed of light in vacuum, need not remain constant during a Big Crunch, especially in the time interval smaller than that in which measurement may never be possible (one unit of Planck time, roughly 10−43 seconds) spanning or bracketing the point of inflection.
1.5 Matter before the Big Bang
It is difficult to make definitive statements about the existence of elementary particles, as described by the Standard Model, before the Big Bang. Our current understanding of the universe, including the behaviour of elementary particles, is based on observations and data from the time immediately following the Big Bang.
The Standard Model of particle physics describes the fundamental particles and forces in the universe, including the electromagnetic, weak, and strong nuclear forces. It is a highly successful framework that has been extensively tested and verified through numerous experiments.
However, our understanding of the universe during the earliest moments of the Big Bang is limited, as the conditions at that time were far more extreme than what we can recreate in laboratories. Some theories, like cosmic inflation and quantum fluctuations, suggest that the universe's initial state may have involved exotic particles or other phenomena not described by the Standard Model. In these scenarios, the elementary particles we know today would have emerged as the universe cooled and expanded.
Additionally, at extremely high energies and temperatures, like those found in the early universe, particles and forces can unify, meaning that the distinctions between the known particles and forces may not have existed in the same way as they do today. This is the basis for the concept of Grand Unified Theories (GUTs), which attempt to describe the unification of forces and particles at these extreme conditions.




1 BEFORE THE BIG BANG
1.1 General
Pre-Big Bang cosmology explores the universe's origin before the Planck epoch, when the universe was younger than 10⁻⁴³ s. The conditions during this period were so extreme that general relativity and quantum mechanics, the two pillars of modern physics, are not sufficient to describe the state of the universe.
One of the goals of pre-Big Bang cosmology is to find alternative scenarios that could explain the universe's origins while addressing the limitations of standard Big Bang theory, such as the initial singularity problem. These scenarios are highly speculative, but they provide a conceptual framework for investigating the universe's state before the Planck epoch:
-
Bouncing Cosmology: In this scenario, the universe undergoes a series of cycles consisting of expansion and contraction phases. The universe's current expansion phase, which began with the Big Bang, could have been preceded by a contracting phase. The transition between these two phases is referred to as the "bounce." Bouncing cosmology might have avoided the initial singularity and provided a finite history before the Planck epoch. Examples include ekpyrotic and cyclic models.
-
String Cosmology: Inspired by string theory, this scenario suggests that the universe's origin could be rooted in the interactions of fundamental strings. A pre-existing string structure or configuration may have produced the universe during the Planck epoch. String cosmology might reveal a different cosmic history before the Planck epoch while providing insights into the nature of spacetime at the most fundamental level.
-
Quantum Cosmology: Quantum cosmology applies quantum mechanics principles to the entire universe, offering a possible description of the universe's initial state before the Planck epoch. In this approach, the universe's initial state could be represented by a wave function that evolves according to the laws of quantum mechanics. One example is the Hartle-Hawking initial state, which proposes a smooth, Euclidean geometry for the initial state of the universe without singularities.
It is essential to emphasise that these pre-Big Bang cosmological scenarios remain speculative and lack direct experimental evidence. As the scientific community develops a more comprehensive framework that unifies general relativity and quantum mechanics, our understanding of the universe's origins before the Planck epoch may improve.


[3]

[6]
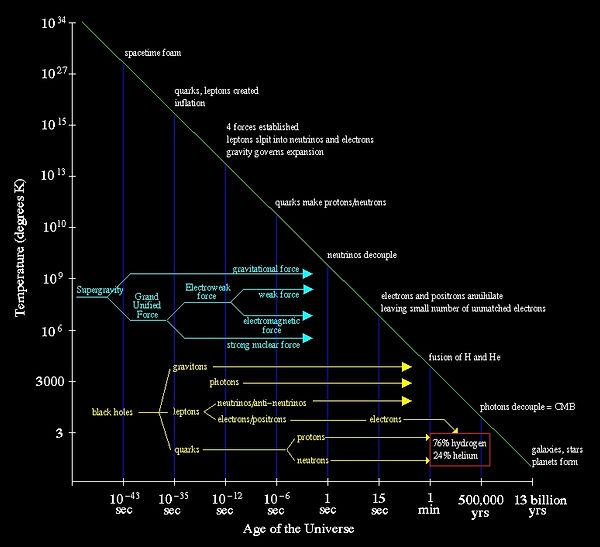
[8]

[13]


[1]
Diagram showing the place of quantum gravity in the hierarchy of physics theories
[2]

[4]
Wormholes, tunnels through the fabric of spacetime that connect widely separated locations, are predicted by Einstein’s general theory of relativity. Some physicists think that wormholes could connect black holes in space, possibly providing a clue to the mysteries of quantum entanglement and how to merge general relativity with quantum mechanics.

[1]



[1]
References
[1] Wikipedia
[3] Different Models of the Universe That Revise the Big Bang Theory. Leonard Kelley (2022) Owlcation
[4] Robert Roy Britt. Space.com
[5] Science News. STOCKERNUMBER2/SHUTTERSTOCK
[6] F. Vidotto/University of the Basque Country
[7] arXiv.org
[8] Course HC209 21st Century Science. Univerity of Oregon. Prof. James Schombert
[9] Veneziano, G. (1998-02-09). "A Simple/Short Introduction to Pre-Big-Bang Physics/Cosmology". arXiv:hep-th/9802057
[10] Khoury, Justin; Ovrut, Burt A.; Steinhardt, Paul J.; Turok, Neil (2001). "The Ekpyrotic Universe: Colliding Branes and the Origin of the Hot Big Bang". Physical Review D. 64 (12): 123522. arXiv:hep-th/0103239. Bibcode:2001PhRvD..64l3522K. doi:10.1103/PhysRevD.64.123522. S2CID 374628.
[11] Ovrut, Burt A.; Khoury, Justin; Buchbinder, Evgeny I. (2008). "Non-Gaussianities in New Ekpyrotic Cosmology". Physical Review Letters. 100 (17): 171302. arXiv:0710.5172. Bibcode:2008PhRvL.100q1302B. doi:10.1103/PhysRevLett.100.171302. PMID 18518270. S2CID 2949857.
[12] Juvela, M.; Jones, W. C.; Jaffe, T. R.; Jaffe, A. H.; Huffenberger, K. M.; Hovest, W.; Hornstrup, A.; Holmes, W. A.; Hobson, M. (2014). "Planck 2013 Results. XXIV. Constraints on primordial non-Gaussianity". Astronomy & Astrophysics. 571: A24. arXiv:1303.5084. Bibcode:2014A&A...571A..24P. doi:10.1051/0004-6361/201321554. S2CID 118603303.
[13] Ekpyrotic Nongaussianity: A Review. Jean-Luc Lehners. 2010. DOI:
[14] Ashtekar, Abhay (2009). "Loop Quantum Cosmology: An Overview". Gen. Rel. Grav. 41 (4): 707–741. arXiv:0812.0177. Bibcode:2009GReGr..41..707A. doi:10.1007/s10714-009-0763-4. S2CID 115155250
[15] Bojowald, Martin (2005). "Loop Quantum Cosmology". Living Reviews in Relativity. 8 (1): 2. arXiv:gr-qc/0502091. Bibcode:2005LRR.....8....2A. doi:10.12942/lrr-2005-2. PMC 5253932. PMID 28163646
[16] On (Cosmological) Singularity Avoidance in Loop Quantum Gravity, Johannes Brunnemann, Thomas Thiemann, Class. Quantum Grav. 23 (2006) 1395-1428.
[17] Unboundedness of Triad -- Like Operators in Loop Quantum Gravity, Johannes Brunnemann, Thomas Thiemann, Class. Quantum Grav. 23 (2006) 1429-1484.
[18] Easther, R.; Maeda, Kei-ichi; Wands, D. (1996). "Tree-level string cosmology". Physical Review D. 53 (8): 4247–4256. arXiv:hep-th/9509074. Bibcode:1996PhRvD..53.4247E. doi:10.1103/PhysRevD.53.4247. PMID 10020421. S2CID 8124718.
[19] Donoghue, John F. (1995). "Introduction to the Effective Field Theory Description of Gravity". In Cornet, Fernando (ed.). Effective Theories: Proceedings of the Advanced School, Almunecar, Spain, 26 June–1 July 1995. Singapore: World Scientific. arXiv:gr-qc/9512024. Bibcode:1995gr.qc....12024D. ISBN 978-981-02-2908-5
[20] Barvinsky, Vilkovisky, A.O, G.A (1983). "The generalized Schwinger-DeWitt technique and the unique effective action in quantum gravity". Phys. Lett. B. 131 (4–6): 313–318. Bibcode:1983PhLB..131..313B. doi:10.1016/0370-2693(83)90506-3.
[21] Barvinsky, Vilkovisky, A.O, G.A (1985). "The Generalized Schwinger-DeWitt Technique in Gauge Theories and Quantum Gravity". Phys. Rep. 119 (1): 1–74. Bibcode:1985PhR...119....1B. doi:10.1016/0370-1573(85)90148-6
[22] Barvinsky, Vilkovisky, A.O, G.A (1987). "Beyond the Schwinger-Dewitt Technique: Converting Loops Into Trees and In-In Currents". Nucl. Phys. B. 282: 163–188. Bibcode:1987NuPhB.282..163B. doi:10.1016/0550-3213(87)90681-X
[23] Barvinsky, Vilkovisky, A.O, G.A (1990). "Covariant perturbation theory. 2: Second order in the curvature. General algorithms". Nucl. Phys. B. 333: 471–511. doi:10.1016/0550-3213(90)90047-H
[24] Calmet, Kuipers, Xavier, Folkert (2021). "Quantum gravitational corrections to the entropy of a Schwarzschild black hole". Phys. Rev. D. 104 (6): 6. arXiv:2108.06824. Bibcode:2021PhRvD.104f6012C. doi:10.1103/PhysRevD.104.066012. S2CID 237091145
[25] Campos Delgado, Ruben (2022). "Quantum gravitational corrections to the entropy of a Reissner-Nordström black hole". Eur. Phys. J. C. 82 (3): 272. Bibcode:2022EPJC...82..272C. doi:10.1140/epjc/s10052-022-10232-0. S2CID 247824137
[26] Zinn-Justin, Jean (2007). Phase transitions and renormalization group. Oxford: Oxford University Press. ISBN 9780199665167. OCLC 255563633.
[27] Hawking, Stephen. "The Beginning of Time". Archived from the original on 6 October 2014. Retrieved 10 March 2014
[28] Dastidar, Samriddhi (3 March 2018). "Stephen Hawking Claims To Know What Happened Before The Big Bang". TechTimes.com. Retrieved 3 March 2018.
[29] Specktor, Brandon (2 March 2018). "Stephen Hawking on What Happened Before the Big Bang". LiveScience. Retrieved 3 March 2018.
[30] John D. Barrow, The Origin of the Universe: To the Edge of Space and Time, Basic Books, 1997.










