General
Gluons are fundamental particles in the Standard Model of particle physics, which describes the fundamental forces and particles in the universe. Specifically, gluons are the force carriers of the strong nuclear force, which is responsible for holding quarks together to form protons, neutrons, and other particles composed of quarks, such as mesons and baryons.
Gluons are massless and electrically neutral particles that mediate the strong force between quarks, which are the building blocks of protons, neutrons, and other hadrons. The strong force is one of the four fundamental forces of nature, alongside electromagnetism, the weak force, and gravity.
Unlike the electromagnetic force, which is mediated by photons, the strong force is unique in that it has a property called color charge, which comes in three types: red, green, and blue, as well as their corresponding anticolors: antired, antigreen, and antiblue. Quarks carry one of these color charges, while gluons carry a combination of a color and an anticolor charge.
One of the distinctive features of the strong force is its property of confinement, which means that quarks cannot exist in isolation but are always bound together to form color-neutral particles due to the increasing strength of the strong force at large distances. Gluons play a crucial role in mediating this force, constantly exchanging gluons between quarks, which creates the strong force field that binds them together.
Properties of Gluons
Masslessness:
Theoretical Foundations:
Gluons are integral components of quantum chromodynamics (QCD), the theory governing the strong nuclear force, which binds quarks together to form hadrons such as protons and neutrons. In the framework of QCD, gluons are massless force carriers analogous to photons in electromagnetism. Theoretical formulations of QCD, rooted in gauge theories and quantum field theory, predict the masslessness of gluons. The mathematical framework of QCD has been extensively tested and validated through various experimental observations and precision calculations. Gluons’ masslessness is a consequence of the symmetries and dynamics of the strong force as described by QCD.
Masslessness in the Standard Model:
Within the Standard Model of particle physics, the mechanism responsible for imparting mass to particles is the Higgs mechanism. This mechanism relies on the Higgs field, which interacts with particles carrying electric charge, such as quarks and leptons. Gluons, being electrically neutral, do not interact with the Higgs field and thus do not acquire mass through the Higgs mechanism. Consequently, within the framework of the Standard Model, gluons are considered massless particles. This understanding is consistent with the experimental evidence and theoretical predictions regarding the behavior of gluons within the Standard Model.
Experimental Evidence:
Experimental studies, including those conducted at particle accelerators such as the Large Hadron Collider (LHC), have provided strong evidence supporting the masslessness of gluons. High-energy collisions involving gluons, such as proton-proton collisions at the LHC, would exhibit deviations from theoretical predictions if gluons possessed mass. However, experimental observations have consistently aligned with the predictions of massless gluons. Various high-precision experiments and analyses have confirmed the masslessness of gluons, reinforcing the theoretical framework of the Standard Model and quantum chromodynamics.
Consequences of Masslessness:
The masslessness of gluons has profound implications for the behavior of the strong force and the dynamics of particle interactions. Gluons, lacking mass, travel at the speed of light and mediate the strong force between quarks within hadrons. This property enables the strong force to act over long distances and play a pivotal role in binding quarks together within protons, neutrons, and other hadrons. Furthermore, the absence of gluon mass contributes to the phenomenon of asymptotic freedom, wherein quarks and gluons behave as nearly free particles at high energies or short distances, leading to unique phenomena observed in particle collisions and interactions.
Color Charge
In the context of the strong nuclear force and quantum chromodynamics (QCD), the concept of color charge is a fundamental aspect that describes the interactions between quarks and gluons.
Color Charge:
In QCD, quarks possess a property known as color charge, which is completely different from the everyday notion of color. The term "color" is used metaphorically to represent the three types of color charge: red, green, and blue. Each of these colors corresponds to a different type of charge. Anti-quarks carry anticolor charge: antired, antigreen, and antiblue. Gluons also carry color charge, but unlike quarks, they can carry a mixture of color and anticolor charges.
Confinement:
One of the most important consequences of color charge is the phenomenon of confinement. According to QCD, the strong force between quarks increases as they are pulled apart. At a certain distance, it becomes energetically favorable to create new quark-antiquark pairs, resulting in the formation of color-neutral hadrons (such as mesons and baryons). This phenomenon prevents the observation of isolated quarks in nature, a concept known as quark confinement.
Gluon Interaction:
Gluons mediate the strong force between quarks by carrying and exchanging color charge. Gluons are unique in that they interact with other gluons and quarks, leading to complex interactions within the nucleus of an atom. Gluons carry a combination of color and anticolor charges, allowing them to couple to quarks and other gluons.
Chromodynamics and Quantum Field Theory:
The description of the strong force in terms of color charge is a manifestation of the principles of quantum field theory. Quantum chromodynamics (QCD) is the quantum field theory that describes the strong interaction and the behavior of quarks and gluons. In QCD, the interactions between quarks and gluons are mediated by the exchange of virtual gluons, leading to the binding of quarks into hadrons.
Spin
In quantum mechanics, spin is an intrinsic property of elementary particles, including gluons. It is a fundamental aspect of particle physics and is often described as a form of angular momentum, although it does not correspond to literal spinning motion as in classical mechanics.
Intrinsic Angular Momentum:
Spin is an intrinsic property of elementary particles, much like mass or charge. It is not associated with any physical rotation in space but rather represents an inherent angular momentum. Gluons, like other elementary particles such as electrons and quarks, possess spin.
Quantization of Spin:
Spin is quantized in quantum mechanics, meaning it can only take on certain discrete values. For fermions (particles with half-integer spin), such as quarks, electrons, and neutrinos, spin can take values of 1221 (spin-up) or −12−21 (spin-down). Gluons, as bosons, have integer spin. They are characterized by a spin value of 1.
Effects of Spin:
Spin influences the behavior of particles in various physical phenomena, including their interactions with external fields and other particles.
In the case of gluons, their spin of 1 contributes to the way they interact with quarks and other gluons through the strong force. The spin of gluons plays a role in determining the quantum numbers of particles resulting from strong interactions, such as mesons and baryons.
Experimental Detection:
Spin is experimentally observed through various techniques, including measurements of the angular distributions of decay products in particle collisions. Experiments in high-energy physics, such as those conducted at particle colliders like the Large Hadron Collider (LHC), provide insights into the spin properties of elementary particles, including gluons.
Role of Gluons in the Strong Force
Gluons play a fundamental role in mediating the strong force, also known as the strong nuclear force or color force, which is one of the four fundamental forces in nature. Here's an explanation of the role of gluons in the strong force:
Mediating the Strong Force:
The strong force is responsible for binding quarks together to form protons, neutrons, and other hadrons, as well as for holding these hadrons together in atomic nuclei. Gluons are the force carriers of the strong force, similar to how photons are the force carriers of the electromagnetic force.
Carrying Color Charge:
Quarks, which are the building blocks of hadrons, carry a property known as color charge, which is distinct from the everyday concept of color. Gluons also carry color charge, which is analogous to the color charge of quarks. Gluons interact with quarks by exchanging color charge, thereby mediating the strong force between quarks.
Confinement:
One of the most important consequences of the strong force is quark confinement, which prevents the isolation of individual quarks.
The strong force between quarks increases as they are pulled apart, making it energetically favorable to create new quark-antiquark pairs, resulting in the formation of color-neutral hadrons. Gluons play a crucial role in the confinement of quarks by mediating the strong force and facilitating the creation of new quark-antiquark pairs.
Asymptotic Freedom:
At short distances or high energies, the strong force between quarks and gluons weakens, a phenomenon known as asymptotic freedom. Asymptotic freedom allows quarks and gluons to behave almost as free particles in high-energy collisions, enabling scientists to study the properties of the strong force at short distances.
Gluon Self-Interactions:
Gluons can interact with each other through self-interactions, leading to complex dynamics within the strong force.
Gluon-gluon interactions contribute to the non-linear behavior of the strong force, resulting in phenomena such as gluon jets in high-energy collisions.
Explanation of the strong nuclear force
Mediation of the strong force
Gluons facilitate the interaction between quarks by carrying and exchanging the strong force, also known as the color force. Here's how gluons mediate the interaction between quarks:
Carrying Color Charge:
Quarks, which are elementary particles that make up protons, neutrons, and other hadrons, possess a property known as color charge.
Gluons, the force carriers of the strong force, also carry color charge. However, unlike quarks, gluons can carry a combination of a color and an anticolor charge. Gluons interact with quarks by exchanging color charge, which allows them to mediate the strong force between quarks.
Exchange of Virtual Gluons:
In the quantum field theory framework of quantum chromodynamics (QCD), the strong force between quarks is mediated by the exchange of virtual gluons. Quarks within hadrons continuously exchange virtual gluons with one another, creating a dynamic and complex interaction network.
The exchange of gluons between quarks results in the binding of quarks together, forming stable hadrons such as protons, neutrons, and mesons.
Confinement and Asymptotic Freedom:
Gluons play a crucial role in two important phenomena related to the strong force: confinement and asymptotic freedom. Quark confinement refers to the inability to observe isolated quarks in nature. Gluons, by mediating the strong force, contribute to the binding of quarks into color-neutral hadrons. Asymptotic freedom describes the weakening of the strong force at short distances or high energies. Gluons and quarks behave almost as free particles in such extreme conditions, allowing scientists to study the properties of the strong force at short distances.
Gluon Self-Interactions:
Gluons can also interact with each other through self-interactions, contributing to the non-linear behavior of the strong force. Gluon-gluon interactions give rise to phenomena such as gluon jets in high-energy particle collisions, which are important signatures for understanding the dynamics of the strong force.
Confinement
The phenomenon where quarks are bound together due to the strong force, resulting in the formation of color-neutral hadrons, is a central concept in the theory of quantum chromodynamics (QCD). This phenomenon is known as quark confinement. Here's a detailed explanation:
Color Charge and Strong Force:
Quarks possess a property called color charge, which is distinct from the everyday notion of color. The term "color" is used metaphorically in particle physics to represent the three types of color charge: red, green, and blue. Gluons, the force carriers of the strong force, also carry color charge. Gluons can interact with quarks by exchanging color charge, mediating the strong force between quarks. The strong force is responsible for binding quarks together to form composite particles known as hadrons, which include protons, neutrons, and mesons.
Confinement:
Quark confinement is the principle that states that isolated quarks cannot be observed in nature. Quarks are always bound together to form color-neutral particles due to the increasing strength of the strong force at large distances.
As quarks are pulled apart, the energy stored in the strong force field between them increases. At some critical separation distance, the energy becomes so high that it is more favorable for new quark-antiquark pairs to be created from the vacuum, forming color-neutral hadrons instead of isolated quarks.
Formation of Hadrons:
The most common types of hadrons are baryons (e.g., protons and neutrons) and mesons. Baryons consist of three quarks, while mesons consist of a quark-antiquark pair. The strong force binds quarks together within hadrons, creating color-neutral combinations that do not violate the principle of color charge conservation. In baryons, the combined color charges of the three quarks cancel each other out, resulting in a color-neutral particle. Similarly, mesons consist of a quark and an antiquark with color charges that cancel each other out.
Experimental Evidence:
Quark confinement has been supported by experimental observations and theoretical calculations in high-energy physics experiments, including those conducted at particle colliders such as the Large Hadron Collider (LHC). Experimental evidence indicates that quarks are always confined within color-neutral hadrons and cannot be observed as isolated particles.
Quantum Chromodynamics (QCD)
Quantum Chromodynamics (QCD) stands as a cornerstone of modern particle physics, providing a comprehensive framework for understanding the strong nuclear force—one of the four fundamental forces governing the universe. Here, we delve into the structured and intricate nature of QCD:
Foundational Concepts of QCD:
QCD is rooted in the concept of color charge, a property analogous to electric charge in electromagnetism. Quarks, the elementary constituents of protons, neutrons, and other hadrons, carry one of three "colors" (red, green, or blue), while antiquarks carry corresponding anticolors. Gluons, the mediators of the strong force, also possess color charge, unlike photons, which mediate the electromagnetic force. Gluons interact not only with quarks but also with each other, contributing to the complexity of the strong interaction.
Properties of the Strong Force:
QCD exhibits two fundamental properties: asymptotic freedom and confinement.
Asymptotic freedom describes the behavior of the strong force at high energies or short distances, where quarks and gluons behave almost independently. This property is a result of QCD's renormalization group equations and enables perturbative calculations in certain regimes. Confinement, on the other hand, is the phenomenon where quarks are bound within color-neutral hadrons. As quarks are separated, the energy stored in the strong force field increases, ultimately leading to the formation of new quark-antiquark pairs, resulting in hadron formation.
Theoretical Approaches and Techniques:
While perturbative methods are applicable in high-energy regimes, non-perturbative methods are necessary for understanding the strong force at low energies and long distances. Lattice QCD, a numerical technique, discretizes QCD equations on a lattice, allowing researchers to explore the non-perturbative regime. Additionally, effective field theories and large-N expansions provide alternative approaches to understanding the intricate dynamics of QCD.
Experimental Validation:
Experimental studies at high-energy particle accelerators, such as the Large Hadron Collider (LHC), play a crucial role in testing and validating QCD predictions. Measurements of hadron production, jet formation, and other QCD phenomena are compared with theoretical calculations based on QCD principles, providing essential insights into the strong interaction.
Gluon-gluon interactions
The self-interactions of gluons are a fundamental aspect of Quantum Chromodynamics (QCD), the theory describing the strong nuclear force. Here's a discussion of how these self-interactions contribute to the complexity of QCD:
Mediating the Strong Force:
Gluons are the force carriers of the strong interaction, analogous to photons in electromagnetism. In QCD, gluons interact not only with quarks but also with each other. This property distinguishes the strong force from electromagnetism, where photons do not self-interact.
Gluon Self-Coupling:
Gluons carry color charge, allowing them to interact with each other through the exchange of gluons. The self-interaction of gluons arises from the non-Abelian nature of the SU(3) gauge group, which is the symmetry group of QCD. In simpler terms, gluons can carry combinations of color and anticolor charges, allowing for gluon-gluon interactions. These self-interactions lead to the nonlinearity of the QCD equations, making analytical solutions difficult to obtain except in very limited cases.
Effects on Strong Force Dynamics:
Gluon self-interactions contribute to the non-linear behavior of the strong force. The self-interactions of gluons play a crucial role in phenomena such as gluon confinement, where gluons cannot exist in isolation but are always bound together with quarks to form color-neutral hadrons. Gluon self-interactions also affect the behavior of gluons in high-energy collisions, leading to the formation of gluon jets and other complex final-state configurations.
Challenges and Complexity:
The self-interactions of gluons introduce significant complexity to the theoretical description of QCD. Calculating gluon-gluon interactions analytically is challenging due to the nonlinearity of the equations and the large number of possible interactions. Instead, physicists rely on numerical simulations, such as lattice QCD, to study gluon self-interactions and their effects on strong force dynamics.
Experimental Signatures:
Experimental observations, particularly in high-energy particle collisions, provide valuable insights into gluon self-interactions. Measurements of jet formation, hadronization processes, and other QCD phenomena offer experimental validation of theoretical predictions regarding gluon self-interactions.
Experimental Evidence for Gluons
Experiments and observations in particle physics have provided compelling evidence supporting the existence and properties of gluons, the force carriers of the strong nuclear force. Here are some key experiments and observations:
Deep Inelastic Scattering (DIS):
One of the landmark experiments that provided evidence for the existence of gluons was deep inelastic scattering, conducted at particle accelerators such as the Stanford Linear Collider (SLC) and the European Organization for Nuclear Research (CERN). In deep inelastic scattering experiments, high-energy electrons or muons are scattered off protons or neutrons. By studying the scattered particles' momentum and angles, physicists can probe the internal structure of the proton or neutron. These experiments revealed that the structure functions of protons and neutrons, as measured in deep inelastic scattering, exhibited scaling behavior predicted by QCD, providing indirect evidence for the existence of gluons.
Hadron Colliders and Gluon Jets:
Hadron colliders, such as the Tevatron at Fermilab and the Large Hadron Collider (LHC) at CERN, have provided direct evidence for gluons through the observation of gluon jets.
Gluon jets are collimated sprays of particles produced when a gluon emitted from a high-energy collision undergoes hadronization, the process by which quarks and gluons bind together to form color-neutral hadrons.
The detection of gluon jets in collision events at hadron colliders confirms the existence of gluons and their role in strong interactions.
Heavy Quarkonia Production:
The production of heavy quarkonia, such as charmonium (composed of a charm quark and an anticharm quark) and bottomonium (composed of a bottom quark and an antibottom quark), in high-energy collisions also provides evidence for the existence of gluons.
The strong force mediated by gluons plays a crucial role in binding heavy quark-antiquark pairs together to form quarkonia states. The observation of these states in collider experiments confirms the existence of gluons and their interaction with heavy quarks.
Lattice QCD Calculations:
Lattice QCD, a numerical technique used to solve QCD equations on a discrete lattice, provides valuable insights into the properties of gluons and their interactions with quarks.
Lattice QCD calculations have successfully reproduced experimental results related to gluon and quark interactions, supporting the validity of QCD as the theory of the strong force.
Related Papers4 (See below in “Theoretical Aspects”)
Techniques such as deep inelastic scattering and hadron colliders, exemplified by the Large Hadron Collider, represent powerful tools in the study of gluons and the strong nuclear force. Through these techniques, physicists continue to deepen our understanding of the fundamental particles and forces that govern the universe, shedding light on the intricate nature of gluons and their role in shaping the fabric of reality.
Theoretical Aspects
Perturbative QCD
The perturbative approach to Quantum Chromodynamics (QCD) calculations is a powerful method used to study gluon interactions at high energies. In this approach, calculations are performed using perturbation theory, which involves expanding physical quantities in terms of a small parameter, typically the strength of the coupling constant, and computing them order by order.
Asymptotic Freedom and Perturbative QCD:
QCD exhibits a remarkable property known as asymptotic freedom, where the strength of the strong force decreases at short distances or high energies. At very high energies, quarks and gluons behave almost as free particles, allowing perturbative methods to be applied. This is in contrast to the low-energy regime, where the strong force becomes strong and non-perturbative effects dominate.
Perturbative Expansion in QCD:
Perturbative QCD calculations involve expanding physical observables, such as scattering amplitudes or cross-sections, in powers of the strong coupling constant αs. The strong coupling constant represents the strength of the interaction between quarks and gluons. At high energies, αs is small, making perturbative expansions feasible. The perturbative expansion is typically carried out using Feynman diagrams, graphical representations that encode the interactions between quarks and gluons at different orders of the expansion.
Feynman Diagrams in QCD:
Feynman diagrams depict particle interactions as lines connecting vertices, with each vertex representing a point where particles interact. In QCD, Feynman diagrams include quark and gluon lines, with gluons mediating the strong force interactions between quarks. The complexity of QCD Feynman diagrams increases with the number of quarks and gluons involved and the order of the perturbative expansion.
Higher-Order Corrections and Renormalization:
Perturbative QCD calculations involve summing over an infinite series of Feynman diagrams at each order of the expansion. Higher-order corrections to observables arise from additional diagrams involving more interactions between quarks and gluons. To ensure that physical predictions are meaningful, calculations must include renormalization, a procedure that removes divergences and incorporates the effects of quantum fluctuations.
Applications and Phenomenology:
Perturbative QCD calculations have been applied to various phenomena in high-energy particle physics, including jet production, deep inelastic scattering, and hadron collisions.
These calculations provide crucial predictions that can be tested against experimental data from particle colliders such as the Large Hadron Collider (LHC), enabling precision tests of QCD and the Standard Model.
Lattice QCD
Lattice QCD is a powerful non-perturbative approach used to study Quantum Chromodynamics (QCD), the theory of the strong nuclear force, on a discrete grid. In lattice QCD, spacetime is discretized into a finite lattice, allowing physicists to perform numerical simulations and solve QCD equations using computational techniques.
The lattice serves as a discrete representation of spacetime, with points on the lattice corresponding to specific positions in four-dimensional space-time. Quarks and gluons are defined on the lattice sites, and the interactions between them are described by the strong force as dictated by QCD.
By discretizing spacetime, lattice QCD allows physicists to perform calculations that would be otherwise intractable using analytical methods. These calculations provide insights into the behavior of quarks and gluons at low energies and long distances, where perturbative methods are not applicable due to the strong coupling between particles.
Lattice QCD simulations involve solving the QCD equations on the lattice using numerical techniques, such as Monte Carlo methods. These simulations enable researchers to study a wide range of phenomena in QCD, including hadron spectroscopy, quark confinement, and the properties of strongly interacting matter under extreme conditions, such as those found in the early universe or in neutron stars.
Gluon Jets and Hadronization
Gluon Jets
Gluon jets are collimated sprays of particles generated in high-energy particle collisions, typically observed in experiments conducted at particle accelerators like the Large Hadron Collider (LHC). These jets stem from the interactions of quarks and gluons, the elementary constituents governed by Quantum Chromodynamics (QCD), the theory of the strong force.
Origin in High-Energy Collisions:
Gluon jets emerge when high-energy hadrons collide at particle accelerators, converting their kinetic energy into mass in the form of quarks and gluons.
Quark-Gluon Interactions:
Following collision, the released energy gives rise to energetic quarks and gluons, which interact intensely due to the strong force mediated by gluons.
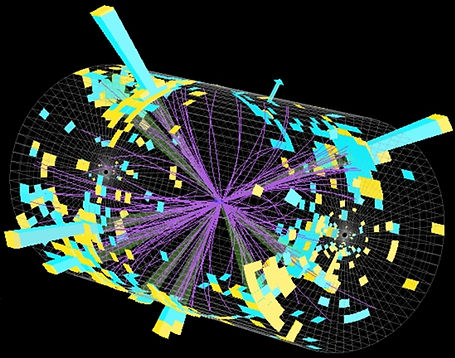
Figure 297 - Gluon JetsFigure 297 - Gluon Jets [7]
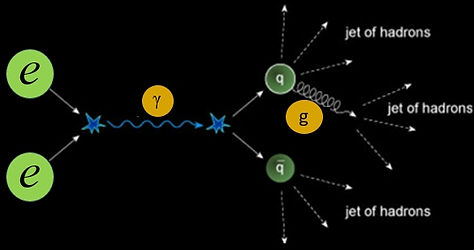
Figure 298 - Quark-Gluon interaction [8]
An electron and a positron mutually annihilate each other to create a virtual photon which subsequently creates a quark–antiquark pair. The quark emits a gluon, shown by the curly line. The energy of the quark, antiquark and gluon are then transformed into many more quarks and antiquarks, which give rise to three jets of hadrons.
Hadronization Process:
As quarks and gluons move apart, the strong force between them intensifies, leading to confinement and the formation of color-neutral hadrons like protons and neutrons, a process known as hadronization.
Experimental Detection:
Gluon jets are identified through sophisticated particle detectors positioned around the collision points. These detectors analyze the properties and trajectories of particles, enabling scientists to reconstruct the characteristics of gluon jets.
Scientific Significance:
Gluon jets provide crucial insights into the behavior of quarks, gluons, and the strong force dynamics governed by QCD. They serve as experimental probes to validate theoretical predictions derived from QCD and facilitate the exploration of new particles and phenomena, including the quark-gluon plasma and exotic states of matter.
Hadronization
The process by which quarks and gluons form color-neutral hadrons, such as protons, neutrons, and mesons, is known as hadronization or hadron formation. Hadronization occurs due to the nature of the strong force, which binds quarks and gluons together into colorless combinations. Here's an overview of the process:
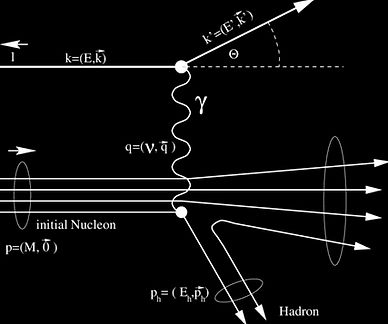
Figure 299 - Hadronization [9]
Quark-Gluon Plasma (QGP) Formation:
In high-energy collisions or extreme conditions, such as those present in the early universe or within neutron stars, quarks and gluons can exist freely due to the high temperatures and densities.
At sufficiently high energies, the strong force becomes weaker, and quarks and gluons behave almost as free particles, forming a state of matter known as quark-gluon plasma (QGP).
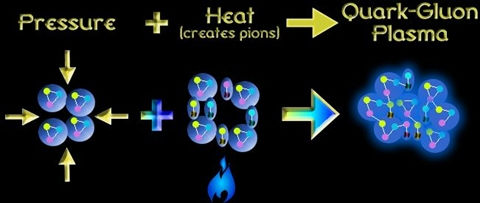
Figure 300 - Quark-Gluon Plasma formation [10]
Confinement and Hadronization:
As the temperature and density decrease or as quarks and gluons move apart, the strong force between them increases. Quarks and gluons cannot exist in isolation due to confinement, a fundamental property of the strong force. Instead, they are confined within color-neutral hadrons.
The process of hadronization involves the conversion of free quarks and gluons into bound states of color-neutral hadrons. The increasing energy associated with the separation of quarks and gluons leads to the creation of new quark-antiquark pairs from the vacuum, ensuring that only color-neutral combinations of quarks and gluons can exist as observable particles.
Formation of Baryons and Mesons:
Baryons, such as protons and neutrons, are color-neutral hadrons composed of three quarks. The combination of three quarks within a baryon ensures that the overall color charge cancels out, resulting in a colorless object. Mesons, on the other hand, are color-neutral hadrons made up of a quark and an antiquark pair. Again, the combination of quark and antiquark ensures overall color neutrality.
Strong Force Dynamics:
The strong force mediated by gluons plays a crucial role in binding quarks together within hadrons. Gluons interact with quarks and other gluons, exchanging color charge and mediating the strong force interactions that bind the constituents of hadrons. The non-linear nature of the strong force leads to complex interactions between quarks and gluons, contributing to the confinement and hadronization process.
Open Questions and Current Research:
Ongoing research in the realm of gluons and the strong force encompasses a wide array of topics, ranging from theoretical investigations to experimental studies. Here are some key areas of focus and unanswered questions:
Gluon Saturation:
Gluon saturation is a phenomenon that occurs at very high energies and densities, where the gluon density becomes so high that nonlinear effects become significant. Understanding gluon saturation is crucial for describing the behavior of partons (quarks and gluons) in high-energy collisions, such as those occurring at the Large Hadron Collider (LHC). Research aims to elucidate the dynamics of gluon saturation and its implications for high-energy particle physics, including the production of jets and other observables.
Quark-Gluon Plasma (QGP):
The quark-gluon plasma (QGP) is a state of matter believed to have existed in the early universe microseconds after the Big Bang and is recreated in heavy-ion collision experiments at facilities like the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC). Understanding the behavior of gluons and quarks within the QGP is a central focus of research, offering insights into the fundamental properties of matter under extreme conditions. Efforts are underway to characterize the QGP's thermodynamic properties, transport coefficients, and phase transitions, providing a deeper understanding of the strong force and the early universe.
Internal Structure of Hadrons:
The internal structure of hadrons, such as protons, neutrons, and mesons, remains an area of active research. Scientists seek to understand the distribution of quarks and gluons within hadrons and their dynamics. Techniques such as lattice QCD calculations and experimental studies using deep inelastic scattering and other probes aim to unravel the intricacies of hadron structure, including the contributions of gluons to their momentum and spin.
Confinement and Strong Force Dynamics:
The mechanism of quark confinement, which prevents the observation of isolated quarks, remains a fundamental puzzle in particle physics. Research efforts seek to elucidate the mechanisms underlying confinement and the role of gluons in binding quarks together to form color-neutral hadrons. Understanding the non-perturbative aspects of the strong force, including its confinement properties, is essential for a complete understanding of QCD and the behavior of matter at the smallest scales.
Why are there eight gluons and not nine?
According to QCD and the standard model of particle physics, quarks carry an SU(3) "color charge" which can be "red", "blue" or "green". The strong nuclear force which binds these together inside the nucleons is mediated by gluons which must carry a color-anticolor charge. This seems to give 9 types of gluon:

Figure 301 - Theoretical Color Combinations with 6 colors
Why are there only eight gluons?
Rather than start with the SU(3) theory, consider first what our knowledge of nature is—upon which we will base the theory. We know that the matter we believe to be composed of quarks (the hadrons) comes in two types: mesons (short lived particles, pions etc.) and baryons (protons, neutrons etc.), both of which have to be strong-force neutral.
Consider the evidence: scattering experiments strongly suggest a meson to be composed of a quark anti-quark pair and a baryon to be composed of three quarks. The famous 3R experiment also suggests that whatever force binds the quarks together has 3 types of charge (called the 3 colors).
Now, into the realm of theory: we are looking for an internal symmetry having a 3-dimensional representation which can give rise to a neutral combination of 3 particles (otherwise no color-neutral baryons). The simplest such statement is that a linear combination of each type of charge (red + green + blue) must be neutral, and following William of Occam we believe that the simplest theory describing all the facts must be the correct one. We now postulate that the particles carrying this force, called gluons, must occur in color anti-color units (i.e. nine of them). BUT, red + blue + green is neutral, which means that the linear combination red anti-red + blue anti-blue + green anti-green must be non-interacting, since otherwise the colorless baryons would be able to emit these gluons and interact with each other via the strong force—contrary to the evidence. So, there can only be EIGHT gluons. This is just Occam's razor again: a hypothetical particle that can't interact with anything, and therefore can't be detected, doesn't exist.
The simplest theory describing the above is the SU(3) one with the gluons as the basis states of the Lie algebra. That is, gluons transform in the adjoint representation of SU(3), which is 8-dimensional.
The physics of color is not understandable if all one knows is that there are 3 colors. One must really understand something about SU(3). SU(3) is the group of 3 × 3 unitary matrices with determinant 1. This is the symmetry group of the strong force. What this means is that, as far as the strong force is concerned, the state of a particle is given by a vector in some vector space on which elements of SU(3) act as linear (in fact unitary) operators. We say the particle "transforms under some representation of SU(3)". For example, since elements of SU(3) are 3 × 3 matrices, they can act on column vectors by matrix multiplication. This gives a 3-dimensional representation of SU(3). Quarks transform under this representation of SU(3), and because it's 3-dimensional we say quarks come in 3 colors: red, green and blue. This is just an amusing way of talking about the 3 column vectors
1
0
0
0
1
0
and
0
0
1
Alternatively, we could let elements of SU(3) act on row vectors by multiplication on the right. Antiquarks transform under that representation, and since it is also 3-dimensional we say they come in three colors as well: anti-red, anti-blue, and anti-green. This is just an amusing way of talking about the 3 row vectors
100
010
and
001
Alternatively, we could let elements of SU(3) act on 3 × 3 hermitian matrices with trace equal to 0, by letting the element g of SU(3) act on the matrix T to give the new matrix gTg−1. The space of 3 × 3 hermitian matrices with trace equal to zero is 8 dimensional. Gluons transform under this representation, so there are 8 gluons.
Some examples of a 3 × 3 hermitian matrix with trace zero are
0 1 0 0 i 0
1 0 0 -i 0 0
0 0 0 0 0 0
If we allow ourselves to take complex linear combinations of these we can get things like
0 1 0
0 0 0
0 0 0
which we could call "red anti-blue" since it has a 1 in the red row (the first row) and the blue column (the second column). Or we could get
0 0 0
1 0 0
0 0 0
which we could call "blue anti-red".
But, no matter how we take complex linear combinations of trace-zero hermitian matrices, we cannot get
1 0 0
0 0 0
0 0 0
since this has trace 1. (I.e., the sum of the diagonal entries is 1: that's what the trace means, the sum of the diagonal entries.) So we cannot really get red anti-red. The closest we can get are things like
1 0 0
0 -1 0
0 0 0
or
1 0 0
0 0 0
0 0 -1
or
0 0 0
0 1 0
0 0 -1
But note, these three are not linearly independent: any one of them is a linear combination of the other two. So we can get stuff like
and so on, but not 3 linearly independent things of this sort, only 2: one less than you might expect. This may have made things seem more, rather than less, mysterious, but in the long run I'm afraid this is what one needs to think about.


Figure 302 - Additive and Subtractive Color Mixing
Measuring the strong force
In September 2023, researchers from the ATLAS experiment at the Large Hadron Collider achieved a breakthrough by measuring the strength of the strong force with unprecedented precision. This achievement holds significant implications for the understanding of fundamental particles and forces in the universe.
The strong force is one of the four fundamental forces of nature, alongside gravity, electromagnetism, and the weak nuclear force. It binds quarks together to form protons, neutrons, and other particles that constitute the building blocks of matter. Measuring the strength of the strong force, quantified by a parameter known as "alpha strong" or αs, is crucial for understanding the behavior of quarks and gluons within hadrons. However, studying the strong force poses challenges due to its unique characteristics.
Unlike other forces, such as electromagnetism, the strong force exhibits counterintuitive behavior. As quarks move apart, the strong force between them increases, making it difficult to directly observe and measure. To overcome this challenge, scientists employ indirect methods and experimental techniques.
At the Large Hadron Collider, experiments like ATLAS and CMS utilize proton-proton collisions to study the strong force. These experiments measure the transverse momentum of particles produced in collisions, such as Z bosons and jets of particles, to extract information about αs.
The recent ATLAS experiment, for instance, measured αs using Z bosons produced in proton-proton collisions. Similarly, the CMS experiment studies jets of particles generated in high-energy collisions to determine the precise strength of the strong force. Improving the precision of αs measurements is essential for advancing our understanding of particle physics and testing theoretical predictions, including those beyond the Standard Model. Precision studies could uncover new phenomena and interactions that lie beyond our current understanding of fundamental physics.
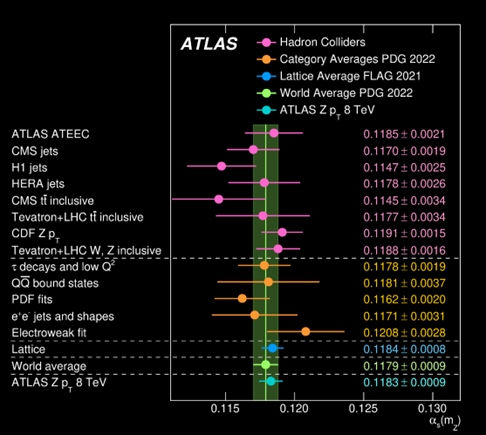
Figure 303 - The new ATLAS value of the strong coupling constant compared with other measurements [11]
Literature
David Blaschke, K. Redlich, Ch. Sasaki, L. Turko. Understanding the origin of matter - Perspectives in Quantum Chromodynamics. Springer (2022) [B075]
John Campbell, Joey Huston, Frank Krauss. The Black Book of Quantum Chromodynamics. Oxford University Press (2018) [B093]
John Collins. Foundations of Perturbative QCD. Cambridge University Press (2023) [B096]
M. Creutz. Quarks, Gluons and Lattices. Cambridge University Press (1985) [B081]
Robin Devenish, Amanda Cooper-Sarkar. Deep Inelastic Scattering. Oxford University Press (2003) [B095]
Takahiro Doi. Lattice QCD Study for the Relation Between Confinement and Chiral Symmetry Breaking. Springer (2018) [B101]
G.V Efimov, M.A Ivanov. The Quark Confinement Model of Hadrons Hardcover. CRC Press (1993) [B091]
Richard D Field. Applications Of Perturbative Qcd. Basic Books (1989) [B098]
Christof Gattringer, Christian B. Lang. Quantum Chromodynamics on the Lattice: An
Jeff Greensite. An Introduction to the Confinement Problem. Springer (2020) [B090]
Walter Greiner, Stefan Schramm, Eckart Stein. Quantum Chromodynamics. Springer (2006) [B076]
M.Y Han. Quarks and Gluons - A Century of Particle Charges. World Scientific (1999) [B079]
J. Kapusta, B. Müller, J. Rafelski. Quark-Gluon Plasma: Theoretical Foundations. Elsevier Science (2003) [B078]
Paul F. Kisak. The Gluon. CreateSpace Independent Publishing Platform (2016) [B080]
John B. Kogut, Mikhail A. Stephanov. The Phases of Quantum Chromodynamics: From Confinement to Extreme Environments. Cambridge University Press (2010) [B092]
Jean Letessier, Johann Rafelski. Hadrons and Quark–Gluon Plasma. Cambridge University Press (2008) [B082]
Huey-Wen Lin, Harvey B. Meyer. Lattice QCD for Nuclear Physics. Springer (2015) [B100]
A H Mueller. Perturbative QCD. World Scientific (1989) [B097]
Robert Nieves. A Quantum Theory of Color Strings: A Palette of Gluons. Independently published (2022) [B089]
Sourav Sarkar, Helmut Satz, Bikash Sinha. The Physics of the Quark-Gluon Plasma. Springer (2010) [B084]
Edward Shuryak. Quark-Gluon Plasma, Heavy Ion Collisions and Hadrons. World Scientific (2024) [B083]
Edward Shuryak. Nonperturbative Topological Phenomena in QCD and Related Theories. Springer (2021) [B099]
Bikash Sinha, Santanu Pal, Sibaji Raha. Quark-Gluon Plasma - Lectures. Springer Verlag (1989) [B085]
Pierre van Baal. Taming the Forces Between Quarks and Gluons. World Scientific (2013) [B086]
Constantinos G. Vayenas, Stamatios N.-A. Souentie. Gravity, Special Relativity, and the Strong Force. Springer (2012) [B094]
Li Yi. Study of Quark Gluon Plasma By Particle Correlations in Heavy Ion Collisions. Springer (2016) [B088]
Francisco J. Ynduráin. The Theory of Quark and Gluon Interactions. Springer (1999) [B087]
References
[1] M. Gell-Mann (1962). "Symmetries of Baryons and Mesons" (PDF). Physical Review. 125 (3): 1067–1084. Bibcode:1962PhRv..125.1067G. doi:10.1103/PhysRev.125.1067. Archived (PDF) from the original on 2012-10-21.. This is without reference to color, however. For the modern usage see Fritzsch, H.; Gell-Mann, M.; Leutwyler, H. (Nov 1973). "Advantages of the color octet gluon picture". Physics Letters B. 47 (4): 365–368. Bibcode:1973PhLB...47..365F. CiteSeerX 10.1.1.453.4712. doi:10.1016/0370-2693(73)90625-4.
[2] B.R. Stella and H.-J. Meyer (2011). "Υ(9.46 GeV) and the gluon discovery (a critical recollection of PLUTO results)". European Physical Journal H. 36 (2): 203–243. arXiv:1008.1869v3. Bibcode:2011EPJH...36..203S. doi:10.1140/epjh/e2011-10029-3. S2CID 119246507
[3] P. Söding (2010). "On the discovery of the gluon". European Physical Journal H. 35 (1): 3–28. Bibcode:2010EPJH...35....3S. doi:10.1140/epjh/e2010-00002-5. S2CID 8289475
[4] Why are there eight gluons?".
[5] W.-M. Yao; et al. (Particle Data Group) (2006). "Review of Particle Physics". Journal of Physics G. 33 (1): 1. arXiv:astro-ph/0601168. Bibcode:2006JPhG...33....1Y. doi:10.1088/0954-3899/33/1/001.
[6] Wikipedia - Gluon
[7] CERN – CMS Experiment 2023
[8] Open University. Particle Physics. 6.1 Gluons
[9] Results from Hermes. Wolfgang Lorenzon. 1998
[10] UC Riverside. Department of Mathematics. Original by James Bottomley and John Baez, 1996.
[11] [1] Image: ATLAS/CERN






