4 INFLATIONARY EPOCH
4.1 General
The inflationary epoch is believed to have occurred between approximately 10⁻³⁶ - 10⁻³² seconds after the Big Bang, and is characterized by a rapid expansion - increasing in size by a factor of at least 10²⁶ - of the universe and that is thought to have been driven by a scalar field, often referred to as the "inflaton field," which permeated the universe during this time. The energy from this field led to the exponential expansion, effectively smoothing out any initial irregularities and setting the stage for the subsequent large-scale structure of the universe.
A key feature of the inflationary epoch is the generation of density fluctuations or quantum fluctuations, which would later act as seeds for the formation of cosmic structures such as galaxies and galaxy clusters. These density fluctuations arose from tiny quantum fluctuations in the inflaton field, which were magnified by the rapid expansion of the universe.
As for the fundamental forces, at the beginning of the inflationary epoch, they are believed to have been unified in a single force. As the universe cooled and expanded, these forces began to separate through a process known as "symmetry breaking." This separation occurred in a series of phase transitions, eventually resulting in the four known fundamental forces: gravity, electromagnetism, the strong nuclear force, and the weak nuclear force.
The first symmetry breaking event is believed to have taken place during the inflationary epoch, separating gravity from the other forces in what is known as "grand unification." This left a single force, the "grand unified force," which included electromagnetism, the strong nuclear force, and the weak nuclear force.
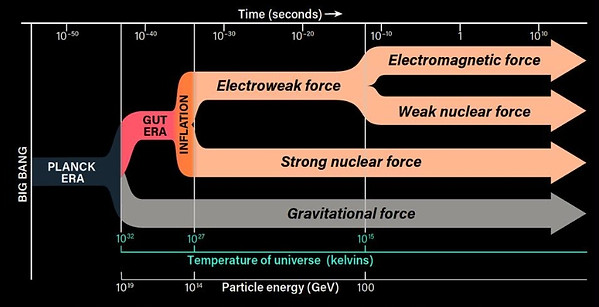
The inflationary epoch came to an end when the inflaton field decayed, converting its energy into particles and radiation that filled the universe. This event, known as reheating, marked the beginning of the hot Big Bang phase, during which the universe continued to expand and cool, eventually allowing for the formation of atoms, stars, and galaxies.
The inflationary model provides a coherent explanation for the observed large-scale uniformity of the cosmic microwave background (CMB) radiation, which is the remnant of the early universe's thermal radiation.


[1]
4.2 Space expands
In a space that expands exponentially (or nearly exponentially) with time, any pair of free-floating objects that are initially at rest will move apart from each other at an accelerating rate, at least as long as they are not bound together by any force. From the point of view of one such object, the spacetime is something like an inside-out Schwarzschild black hole—each object is surrounded by a spherical event horizon. Once the other object has fallen through this horizon it can never return, and even light signals it sends will never reach the first object (at least so long as the space continues to expand exponentially).
In the approximation that the expansion is exactly exponential, the horizon is static and remains a fixed physical distance away. This patch of an inflating universe can be described by the following metric:
ONTBREKENDE FORMULE
This exponentially expanding spacetime is called a de Sitter space, and to sustain it there must be a cosmological constant, a vacuum energy density that is constant in space and time and proportional to Λ in the above metric. For the case of exactly exponential expansion, the vacuum energy has a negative pressure p equal in magnitude to its energy density ρ; the equation of state is p=−ρ.
Inflation is typically not an exactly exponential expansion, but rather quasi- or near-exponential. In such a universe the horizon will slowly grow with time as the vacuum energy density gradually decreases.
See also the item below (The Dark Energy Spectroscopic Instrument (DESI)) regarding the exact expansion of the universe.
4.3 Resolving three major problems in cosmology.
4.3.1 The horizon problem
The horizon problem arises from the fact that the Cosmic Microwave Background (CMB) radiation exhibits a high degree of uniformity (i.e., has nearly the same temperature) across regions that are seemingly too far apart to have ever been in causal contact.
The inflationary theory solves the horizon problem by assuming that the regions of the CMB we observe today were once much closer together, in causal contact with one another, and thus able to exchange energy and reach a thermal equilibrium. During the inflationary period, these regions expanded exponentially, stretching to sizes much larger than the observable universe. This means that, even though these regions are now too far apart to have been in causal contact since the end of inflation, they were once in contact and had time to reach a uniform temperature.
[1]

[1]
4.3.2 The flatness problem
The flatness problem arises from the observed near-flatness of the universe, which means that the overall geometry of the universe is very close to being Euclidean. The flatness problem is closely related to the density parameter (Ω), which is the ratio of the actual mass-energy density of the universe to the critical density required for a flat universe.
In the standard Big Bang model, the density parameter (Ω) evolves over time, and any deviation from a flat universe (Ω = 1) tends to increase as the universe expands. This implies that, for the universe to be observed as nearly flat today, the initial conditions at the time of the Big Bang must have been extraordinarily fine-tuned, with the density parameter being extremely close to 1. This fine-tuning is considered unsatisfactory from a theoretical standpoint, as it lacks a physical explanation and seems highly improbable.
Inflationary cosmology solves the flatness problem by proposing that brief period of rapid exponential expansion. During inflation, any initial curvature of the universe is effectively "stretched out," causing the density parameter (Ω) to be driven very close to 1. This rapid expansion smooths out any initial curvature or inhomogeneities in the universe, resulting in the observed near-flatness.

[1]
The inflationary scenario eliminates the need for extreme fine-tuning of initial conditions, as even if the universe initially had a significant curvature, inflation would have diluted it to the point where the universe would appear nearly flat today. This idea is consistent with current observational data, including the measurements of the Cosmic Microwave Background (CMB) radiation, which show that the universe is indeed very close to being flat.
4.3.3 The magnetic monopole problem
Magnetic monopoles are hypothetical elementary particles that possess a single magnetic charge, either north or south, as opposed to the paired north-south magnetic charges observed in conventional magnets. These particles were predicted to exist by various grand unified theories (GUTs) and some supersymmetric theories, which attempt to unify the fundamental forces of nature at high energies.
In the context of the Big Bang model, the magnetic monopole problem arises from the fact that these theories predict the production of magnetic monopoles during the early stages of the universe. However, the abundance of magnetic monopoles predicted by these theories is much higher than what is observed, as no magnetic monopoles have been detected so far.
Inflationary cosmology offers a solution to the magnetic monopole problem through the rapid exponential expansion of the early universe, known as cosmic inflation. During the brief inflationary period, the universe expanded by many orders of magnitude, effectively diluting the density of magnetic monopoles. This means that even if magnetic monopoles were produced in the early universe, as predicted by grand unified theories, the inflationary expansion would have caused their density to decrease dramatically, making them extremely rare and difficult to detect in the present universe.

[1]
This solution to the magnetic monopole problem is consistent with the fact that no magnetic monopoles have been observed to date, despite extensive experimental searches. However, it is worth noting that the absence of observed magnetic monopoles could also be due to the fact that they may not exist, or that the theories predicting their existence may be incorrect.
4.4 Various models and theories.
As scientists continue to explore the inflationary epoch, various models and theories have been proposed to explain the precise mechanisms and dynamics of this period. Some of these models include chaotic inflation, new inflation, and eternal inflation, each offering unique insights into the early universe's behavior.
4.4.1 Chaotic Inflation
Chaotic inflation is a specific model of cosmic inflation proposed by physicist Andrei Linde in the early 1980's.
In the chaotic inflation model, the exponential expansion of the universe is driven by a scalar field called the inflaton field. The inflaton field is characterized by a potential energy function, which depends on the value of the field. In the context of chaotic inflation, the potential energy function is usually chosen to be a simple power-law or a combination of power-law functions.
The main idea behind chaotic inflation is that, in the very early universe, the inflaton field could have taken on a wide range of initial values, resulting in a highly inhomogeneous and "chaotic" distribution. As the universe expanded, regions with high potential energy underwent rapid, exponential expansion driven by the inflaton field. This inflationary expansion stretched the universe, smoothing out its geometry and density fluctuations, and driving the density parameter (Ω) very close to 1, resulting in the observed near-flatness of the universe.
During the inflationary phase, quantum fluctuations in the inflaton field were stretched and amplified, seeding the formation of the large-scale structure of the universe that we observe today. Once the inflationary phase ended, the inflaton field decayed into the particles that make up the matter and radiation we observe in the universe, initiating the standard hot Big Bang phase.
Linde realized that in fact inflation does not require a plateau in the potential energy diagram, but can in fact happen with a potential energy function as simple as
which in fact describes a non-interacting particle of mass m. If the field φ is started at a large enough value, then sufficient inflation can occur as the scalar field rolls towards φ = 0. Linde initially proposed that the scalar field could start at a large value in some places due to “chaotic" initial conditions. Later he showed that quantum fluctuations can cause these models to also undergo eternal inflation, which will be discussed below, so the question of initial conditions is perhaps irrelevant. [5]
4.4.2 New Inflation
New inflation is a model of cosmic inflation proposed in the early 1980s, independently by Andrei Linde and by Andreas Albrecht and Paul Steinhardt. It builds upon the ideas of the original inflation model, known as "old inflation," which was proposed by Alan Guth in 1980. New inflation sought to address some of the shortcomings of the old inflation model and has contributed to the development of a wide range of subsequent inflationary models, including chaotic inflation and eternal inflation.
In the new inflation model, the early universe undergoes a phase of rapid, exponential expansion driven by the inflaton scalar field, just like in other inflationary models. However, in new inflation, the inflaton field is characterized by a potential energy function that has a flat, plateau-like region near the maximum of the potential. This flat region allows the inflaton field to "slow-roll" down the potential, leading to a longer period of inflation that can more effectively address the horizon, flatness, and magnetic monopole problems.
New inflation differs from chaotic inflation in several key aspects:
-
Initial conditions: in new inflation, the inflaton field is assumed to start near the maximum of its potential, in the flat region. In contrast, chaotic inflation assumes a wide range of initial values for the inflaton field, resulting in a more inhomogeneous and chaotic distribution of the field in the early universe.
-
Potential energy function: the inflaton potential in new inflation is characterized by a flat region near its maximum, which allows for the slow-roll behavior that drives inflation. In chaotic inflation, the potential energy function is typically a simple power-law or a combination of power-law functions, without a flat region near the maximum.
-
Fine-tuning: new inflation requires more fine-tuning of the inflaton potential and initial conditions to achieve the desired slow-roll inflationary phase. Chaotic inflation, on the other hand, is less sensitive to the specific form of the potential and the initial conditions.
4.4.3 Eternal inflation
Eternal inflation is a concept that can emerge from various inflationary models, including new inflation, chaotic inflation, and other models with specific properties. It refers to the idea that some regions of the universe might continue to undergo inflation indefinitely, even as other regions cease to do so. This concept was first proposed by Andrei Linde in the early 1980s and has since been further developed and refined by other researchers.
In the context of the early universe, eternal inflation occurs when quantum fluctuations in the inflaton field – the scalar field that drives inflation – cause some regions of the universe to experience an increase in potential energy. This increase in potential energy leads to a continued phase of rapid, exponential expansion in these regions, while other regions with lower potential energy end their inflationary phase and transition to the standard hot Big Bang phase.
As a result of eternal inflation, a "multiverse" scenario emerges, where many disconnected "bubble" universes are continually formed. Each of these bubbles can have potentially different physical properties and constants, depending on the specific inflationary model and the properties of the inflaton field.

[2]
These models, while offering different perspectives on the inflationary epoch, all contribute to our understanding of this crucial phase in the universe's history. Ongoing research in cosmology and astrophysics is focused on gathering more observational data and refining theoretical models to better comprehend the mechanisms and implications of the inflationary epoch.
In addition to the cosmic microwave background (CMB), other observables, such as the distribution of large-scale structures and the abundance of light elements in the universe, provide vital clues about the inflationary epoch. Future observations, including those from next-generation telescopes and satellite missions, are expected to provide even more accurate measurements, enhancing our understanding of the early universe and ultimately helping us unravel the mysteries of the inflationary epoch.
4.4.4 Wave function of the universe
The singularity theorems, established by Stephen Hawking, Roger Penrose, and others, conclusively demonstrated that the classical Einstein equation indicated that the universe originated in a hot big bang. However, these theorems also revealed that the beginning could not be defined by a classical space-time geometry that followed the Einstein equation with three spatial and one temporal dimension at each point. Instead, they showed that the classical Einstein equation breaks down at the big bang, and with it, the idea that it could be represented by a classical space-time.
In examining the past, researchers found that energy scales near the big bang would have reached a point where space-time geometry fluctuates quantum mechanically without a definite value - quantum gravity. Hawking's earlier work with James Hartle had demonstrated the power of Euclidean geometry in understanding quantum Hawking radiation from evaporating black holes. Consequently, it was natural to attempt using similar techniques to describe the quantum birth of the universe. In 1981, at a conference in the Vatican, Hawking proposed that the universe began with a regular Euclidean geometry with four spatial dimensions, which underwent a quantum transition to a Lorentzian geometry with three spatial and one temporal dimension that we experience today.
For this idea to be solid, a quantum state - a wave function of the universe - was required. Hawking and Hartle realized that this could be the cosmological equivalent of the ground state, constructed as a Euclidean functional integral. This led to the development of the no-boundary wave function or the no-boundary proposal.
In the early 1980s, Hawking built on his work with Gary Gibbons on quantum field theory in de Sitter space-time, demonstrating that inhomogeneities in the early universe could have originated from quantum vacuum fluctuations that expanded during an early inflationary period and eventually collapsed under gravity to create the large-scale structures we observe today. Subsequent observations confirmed these predictions, which count as one of the great achievements of theoretical cosmology, linking the universe's earliest quantum evolution to the matter distribution today. As a result of the growth of fluctuations, the universe also exhibits arrows of time, such as the global increase in thermodynamic entropy.
The no-boundary proposal has had significant impact not only as a successful theory of the origin of the universe's basic structure but also on how we perceive the universe and our place within it. It has led to new understandings in quantum cosmology, arrows of time, our role as observers, formulations of quantum mechanics, and the notion of a "final theory." In his final work in cosmology, Hawking, Hartle, and Thomas Hertog showed that the histories dominating the top-down probabilities in the no-boundary proposal have a regime of so-called eternal inflation where quantum effects dominate the universe's evolution.
Hawking always referred to the theory as a "proposal" for the quantum beginning of the universe. It remains to be seen whether its predictions align with future observations and, if so, whether it is unique in some sense. Regardless of whether the no-boundary proposal proves to be correct or not, Hawking's vision to bring the question of the universe's boundary conditions firmly within the realm of physical sciences and his unwavering pursuit of a simple, manageable quantum theory of the beginning represent a massive conceptual leap forward.
4.4.5 Non-minimally coupled inflation
Non-minimally coupled inflation is an inflationary model in which the constant which couples gravity to the inflaton field is not small. The coupling constant is usually represented by ξ (letter xi), which features in the action (constructed by modifying the Einstein–Hilbert action):
ONTBREKENDE FORMULE
with ξ representing the strength of the interaction between R and Φ, which respectively relate to the curvature of space and the magnitude of the inflaton field.
4.5 Inflationary epoch and Matter
During the inflationary epoch, the behavior of elementary particles is not well-understood due to the extreme energy scales and the conditions that existed at that time. However, based on our current understanding of inflation and particle physics, we can provide a general picture of the behavior of elementary particles during this period.
-
Inflaton field dominance: the inflationary epoch is primarily driven by a scalar field called the inflaton field. The potential energy of the inflaton field dominates the energy density of the universe, causing a rapid exponential expansion. During this time, the inflaton field is the primary component of the universe, and the behavior of elementary particles is influenced by the dynamics of this field.
-
Quantum fluctuations: quantum fluctuations play a crucial role during the inflationary epoch. The rapid expansion of space stretches these fluctuations to macroscopic scales, seeding the initial density perturbations that will later lead to the formation of large-scale structures in the universe. These quantum fluctuations also affect the behavior of elementary particles and their corresponding fields during inflation. However, the detailed dynamics of these fluctuations and their impact on the behavior of elementary particles are still not fully understood.
-
Minimal particle production: during the inflationary epoch, the production of elementary particles is expected to be minimal, as the universe's energy density is dominated by the inflaton field. However, some particle production may occur due to the highly energetic nature of the inflationary period and the interactions between the inflaton field and other fields in the universe.
-
Reheating: the end of the inflationary epoch is marked by a process called reheating, during which the inflaton field decays and transfers its energy to other fields, including those corresponding to the elementary particles described by the Standard Model. It is during this reheating phase that the elementary particles are produced in significant quantities, leading to the hot, dense state of the early universe known as the radiation-dominated era. The behavior of elementary particles during the inflationary epoch is primarily governed by their interactions with the inflaton field and the quantum fluctuations that arise from the highly energetic environment.
It is important to note that our understanding of the behavior of elementary particles during the inflationary epoch is still incomplete, and much of what we know is based on theoretical speculations and models. Further experimental and observational data, as well as advancements in theoretical physics, are needed to refine our understanding of the inflationary epoch and the behavior of elementary particles during this period.
4.6 The Dark Energy Spectroscopic Instrument (DESI)
The Dark Energy Spectroscopic Instrument (DESI) is a cutting-edge scientific tool designed to conduct spectrographic astronomical surveys of distant galaxies. It comprises a focal plane with 5,000 fiber-positioning robots and a bank of spectrographs fed by these fibers. Situated atop Kitt Peak in the Sonoran Desert, Arizona, DESI's main mission is to investigate the expansion history of the universe and the enigmatic nature of dark energy.
Operated by the Lawrence Berkeley National Laboratory and funded by various entities including the US Department of Energy, DESI aims to create detailed three-dimensional maps of matter distribution across vast regions of the universe. These maps will shed light on dark energy, alternative theories to General Relativity, neutrino masses, and the early universe.
Utilizing the baryon acoustic oscillations (BAO) technique, DESI will measure the universe's expansion history by analyzing the clustering patterns of galaxies, quasars, and the intergalactic medium. This technique, identified as crucial in understanding dark energy, enables scientists to extract cosmological distance information with minimal systematic errors.
Endorsed by federal advisory committees and established as a transformative instrument in cosmological research, DESI holds promise in unraveling some of the greatest mysteries surrounding the universe's evolution and fundamental physical laws.

Figure 22 - DESI Telescope
First Results from DESI Make the Most Precise Measurement of Our Expanding Universe [8]
DESI (Dark Energy Spectroscopic Instrument) has achieved a groundbreaking feat by constructing the largest 3D map of the cosmos ever made, covering 11 billion years of cosmic history with unprecedented precision. This milestone allows scientists to measure the expansion history of the universe with a precision better than 1% for the first time, offering profound insights into cosmic evolution. By combining DESI's first-year results with data from other studies, subtle differences with the leading cosmological model, Lambda CDM, have emerged, hinting at potential evolution of dark energy over time.

Figure 23 - DESI has made the largest 3D map of our universe to date. Earth is at the center of this thin slice of the full map. In the magnified section, it is easy to see the underlying structure of matter in our universe. [9]
DESI operates by using galaxies and quasars as cosmic rulers, measuring the apparent size of Baryon Acoustic Oscillations (BAOs) to determine distances to matter in the universe. Its measurements have already surpassed those of previous surveys, providing new perspectives on cosmic dynamics. Additionally, DESI's innovative approach includes a fully blinded analysis, ensuring the integrity of results.
The instrument's success has significant implications for cosmological research, complementing upcoming sky surveys and potentially paving the way for future upgrades. DESI's international collaboration and support from various institutions underscore its importance in advancing our understanding of the universe while acknowledging the significance of the research conducted on Kitt Peak, a site of cultural importance to the Tohono O'odham Nation.
Furthermore, DESI's precision in mapping the expansion history across all 11 billion years of cosmic time, especially in the most distant epoch covering 8-11 billion years in the past, highlights its remarkable capabilities. This measurement of the young universe, although incredibly challenging, has been achieved within just one year of DESI's operations, demonstrating its efficiency compared to its predecessor surveys.
The utilization of galaxies and quasars as cosmic probes offers a multifaceted approach to understanding the universe's expansion history. While galaxies provide valuable insights, the study turns to quasars for more distant observations, utilizing the Lyman-alpha forest technique to extend measurements up to 11 billion years in the past. DESI's collection of 450,000 quasars for these measurements represents a significant leap in observational capabilities, paving the way for even deeper insights into cosmic evolution.
DESI's methodology also stands out for its fully blinded analysis, ensuring the rigor and objectivity of its findings. This approach, coupled with the instrument's unprecedented data collection rate, instills confidence in the robustness of DESI's results and sets a new standard for cosmological research.
Looking ahead, DESI's data will not only complement future sky surveys but also contribute to potential upgrades, as recommended in recent reports. Its impact extends beyond current research endeavors, shaping the future trajectory of cosmology and our understanding of the universe's dynamics.
In recognizing the collaborative effort involving over 900 researchers from 70 institutions worldwide, DESI's significance in advancing cosmological knowledge becomes apparent. The diverse support from institutions and funding bodies further underscores the instrument's importance in pushing the boundaries of scientific exploration.
Moreover, DESI's operations on Kitt Peak carry cultural significance, acknowledging the heritage of the Tohono O'odham Nation. This recognition emphasizes the importance of responsible and respectful scientific inquiry, honoring the land and its indigenous inhabitants.
In summary, DESI's achievements mark a significant milestone in cosmological research, offering unprecedented insights into the universe's evolution and the nature of dark energy. Its groundbreaking capabilities, rigorous methodology, and collaborative spirit pave the way for future discoveries and advancements in our understanding of the cosmos.
Pubications by U.S. Department of Energy Office of Sciente regarding DESI [10]
This chapter provides a curated list of key DESI technical papers useful for understanding and using the DESI data, as well as the Year 1 cosmology and supporting papers released on April 4, 2024.
Papers released with the Early Data Release are available here, and a comprehensive list of DESI publications, including additional science papers, is here.
Year 1 Cosmology Results
The following articles using the DESI Year 1 dataset were released on April 4, 2024. For more context about these papers, please also see the Guide to DESI Year 1 Results webpage.
Key Publications
DESI Collaboration et al., DESI 2024 III: Baryon Acoustic Oscillations from Galaxies and Quasars
DESI Collaboration et al., DESI 2024 IV: Baryon Acoustic Oscillations from the Lyman Alpha Forest
DESI Collaboration et al., DESI 2024 VI: Cosmological Constraints from the Measurements of Baryon Acoustic Oscillations
Supporting Publications: DESI 2024 III
The following articles are supporting publications for DESI 2024 III: Baryon Acoustic Oscillations from Galaxies and Quasars.
Rashkovetskyi et al. (2023), Validation of semi-analytical, semi-empirical covariance matrices for two-point correlation function for early DESI data
Chen et al. (2024), Baryon Acoustic Oscillation Theory and Modelling Systematics for the DESI 2024 results
Paillas, Ding, Chen et al. (2024), Optimal Reconstruction of Baryon Acoustic Oscillations for DESI 2024
Rashkovetskyi et al. (2024), Semi-analytical covariance matrices for two-point correlation function for DESI 2024 data
Mena-Fernandez et al. (2024), HOD-Dependent Systematics for Luminous Red Galaxies in the DESI 2024 BAO Analysis
Garcia-Quintero et al. (2024), HOD-Dependent Systematics in Emission Line Galaxies for the DESI 2024 BAO analysis
Supporting Publications: DESI 2024 IV
The following articles are supporting publications for DESI 2024 IV: Baryon Acoustic Oscillations from the Lyman Alpha Forest.
Ramírez-Pérez et al. (2024), The Lyman-α forest catalogue from the Dark Energy Spectroscopic Instrument Early Data Release
Gordon et al. (2023), 3D correlations in the Lyman-α forest from early DESI data
Filbert et al. (2023), Broad Absorption Line Quasars in the Dark Energy Spectroscopic Instrument Early Data Release
Herrera-Alcantar et al. (2024), Synthetic spectra for Lyman-α forest analysis in the Dark Energy Spectroscopic Instrument
Bault et al. (2024), Impact of Systematic Redshift Errors on the Cross-correlation of the Lyman-α Forest with Quasars at Small Scales Using DESI Early Data
Guy, Gontcho A Gontcho et al. (2024), Characterization of contaminants in the Lyman-alpha forest auto-correlation with DESI
Cuceu et al. (2024), Validation of the DESI 2024 Lyα forest BAO analysis using synthetic datasets
Technical Papers
Data Acquisition and Reduction
-
Spectroscopic Pipeline: Guy et al. (2023), The Spectroscopic Data Processing Pipeline for the Dark Energy Spectroscopic Instrument
-
Redshift Fitting (Redrock): Bailey et al. (in preparation)
-
Fiber Assignment: Raichoor et al. (in preparation)
-
Survey Design and Simulations: Schlafly et al. (2023), Survey Operations for the Dark Energy Spectroscopic Instrument
-
Early Data Release: DESI Collaboration et al. (2023b), The Early Data Release of the Dark Energy Spectroscopic Instrument
Instrumentation
-
Overview: DESI Collaboration et al. (2022), Overview of the Instrumentation for the Dark Energy Spectroscopic Instrument
-
Fiber System: Poppett et al. (in preparation), The Fiber System for the Dark Energy Spectroscopic Instrument
-
Focal Plane: Silber et al. (2023) The Robotic Multiobject Focal Plane System of the Dark Energy Spectroscopic Instrument
-
Optical Corrector: Miller et al. (2023), The Optical Corrector for the Dark Energy Spectroscopic Instrument
-
Spectrograph: Jelinsky et al. (in preparation), The Spectrograph System for the Dark Energy Spectroscopic Instrument
Target Selection and Survey Validation
Overview
DESI Collaboration et al. (2023a), Validation of the Scientific Program for the Dark Energy Spectroscopic Instrument
Myers et al. (2023a), The Target Selection Pipeline for the Dark Energy Spectroscopic Instrument
BGS: Bright Galaxy Survey
Hahn et al. (2023), DESI Bright Galaxy Survey: Final Target Selection, Design, and Validation
Ruiz-Macias et al. (2020), Preliminary Target Selection for the DESI Bright Galaxy Survey
LRG: Luminous Red Galaxies
Zhou et al. (2023), Target Selection and Validation of DESI Luminous Red Galaxies
Zhou et al. (2020), Preliminary Target Selection for the DESI Luminous Red Galaxy (LRG) Sample
ELG: Emission Line Galaxies
Raichoor et al. (2023), Target Selection and Validation of DESI Emission Line Galaxies
Raichoor et al. (2020), Preliminary Target Selection for the DESI Emission Line Galaxy (ELG) Sample
QSO: Quasars
Chaussidon et al. (2023), Target Selection and Validation of DESI Quasars
Yeche et al. (2020), Preliminary Target Selection for the DESI Quasar (QSO) Sample
MWS: Milky Way Survey
Cooper et al. (2022), Overview of the DESI Milky Way Survey
Allende Prieto et al. (2020), Preliminary Target Selection for the DESI Milky Way Survey
Visual Inspection
Lan et al. (2023), The DESI Survey Validation: Results from Visual Inspection of Bright Galaxies, Luminous Red Galaxies, and Emission Line Galaxies
Alexander et al. (2023), The DESI Survey Validation: Results from Visual Inspection of the Quasar Survey Spectra
Imaging Surveys
Dey et al. (2019), Overview of the DESI Legacy Imaging Surveys
Zou et al. (2017), Project Overview of the Beijing-Arizona Sky Survey
4.7 Advised Literature
-
Alan Guth. The Inflationary Universe. This is a classic book by one of the pioneers of inflationary cosmology. Written by the physicist who first proposed the idea of an inflationary epoch, it provides a detailed and accessible introduction to the subject.
-
Edward Kolb and Michael Turner. The Early Universe. This book is a introduction to the early universe, including the inflationary epoch. It covers the history of the universe from the Big Bang to the formation of galaxies and provides a detailed treatment of inflationary cosmology.
-
Andrei Linde. Inflation and Quantum Cosmology. Written by one of the leading experts in inflationary cosmology, this book provides a detailed and technical introduction to the subject. It covers the latest developments in inflationary cosmology and its connection to quantum mechanics.
-
Simon Singh. Big Bang: The Origin of the Universe. This book provides a popular and accessible introduction to the history of the universe, including the inflationary epoch. It covers the latest scientific discoveries and theories, including inflation, and provides a clear explanation of the complex concepts involved.
-
Steven Weinberg. The First Three Minutes. This book is a classic introduction to the early universe, including the inflationary epoch. It provides a clear and concise explanation of the events that occurred in the first moments of the universe and covers the latest scientific discoveries and theories.
-
A. H. Guth. The in inflationary universe: A possible solution to the horizon and flatness problems. Physical Review D, vol. 23, pp. 347{356 (1981)
-
A. D. Linde. A new in inflationary universe scenario: A possible solution of the horizon,flatness, homogeneity, isotropy and primordial monopole problems, Physics Let-ters B, vol. 108, pp. 389{393 (1982)
-
A. Albrecht and P. J. Steinhardt. Cosmology for grand unified theories with radiatively induced symmetry breaking, Physical Review Letters, vol. 48, pp. 1220{1223)
-
Planck 2015 results, XIII: Cosmological parameters, P. A. R. Ade et al. (Planck Collaboration)
-
A. D. Linde. Quantum creation of the inflationary universe. Academy of Sciences of the USSR
-
·J. B. Hartle and S. W. Hawking. Wave function of the Universe. Phys. Rev. D 28, 2960 (1983)
-
Robert M. Wald. Asymptotic behaviour of homogeneous cosmological models in the presence of a positive cosmological constant. Phys. Rev. D 28, 2118(R) (1983)
-
A. D. Sakharov. The initial stage of an expanding universe and the appearance of a nonuniform distribution of matter. (1966)
-
V. F. Mukhanov and G. V. Chibisov. Quantum fluctuations and a non-singular universe. (1981)
-
f matter. A. D. Sakharov (1966)



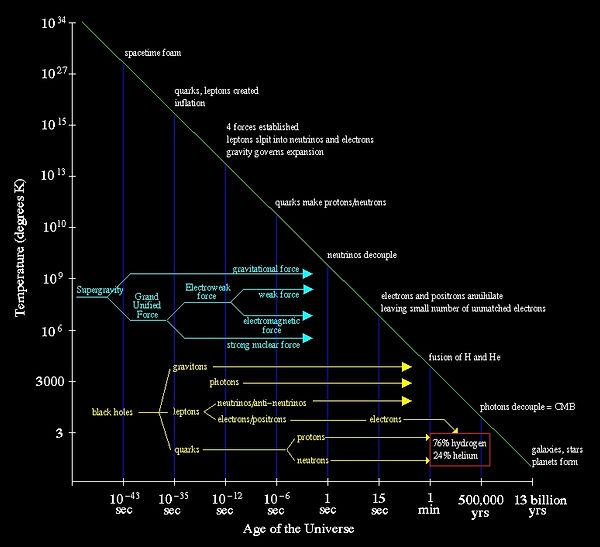
[4]
References
[1] Wikipedia
[2] Inflationary Cosmology. Sergei Winziki. Predictions of Eternal Inflations. Springer Lecture Note
[3] arXiv.org
[4] Course HC209 21st Century Science. Univerity of Oregon. Prof. James Schombert
[5] Alan H. Guth. The New Inflationary Universe. Lecture Notes 10.
[6] Melia, Fulvio (2008). "The Cosmic Horizon". Monthly Notices of the Royal Astronomical Society. 382 (4): 1917–1921. arXiv:0711.4181. Bibcode:2007MNRAS.382.1917M. doi:10.1111/j.1365-2966.2007.12499.x. S2CID 17372406
[7] Melia, Fulvio; et al. (2009). "The Cosmological Spacetime". International Journal of Modern Physics D. 18 (12): 1889–1901. arXiv:0907.5394. Bibcode:2009IJMPD..18.1889M. doi:10.1142/s0218271809015746. S2CID 6565101
[8] Based on Press Release from Birkeley Lab. Lauren Biron, April 4, 2024
[9] Claire Lamman/DESI collaboration; custom color map package by cmastro
[10] Website Dark Energy Spectroscopic Insutrument (https://data.desi.lbl.gov/doc/papers/)










